数学表达式
Input embedding
假设目前输入为 $N$ 个token,经过embedding后,变为 $N \times d_f$ 矩阵,记为 $I$
Positional encoding
对输入的各个token做位置编码,最简单的编码方式是直接将位置向量累加到对应的emdding向量中
输入$N \times d_f$,输出$N \times d_f$
Encoding
Q,K,V
假设目前输入为 $N$ 个token,经过embedding后,变为 $N \times d$ 矩阵,记为 $I$。($d=512$,下面的 $d_{model}$ 也是同样大小) 那么 $Q,K,V$ 可以通过如下计算得到:
\[Q = I \times W^Q\] \[K = I \times W^K\] \[V = I \times W^V\]其中 $W^Q,W^K,W^V$ 分别为 $d \times d_k, d \times d_k, d \times d_v$ 大小的矩阵,$Q,K,V$ 大小为 $N \times d_k, N \times d_k$ 和 $N \times d_v$。
单头注意力
在上一步的基础上,我们继续:
\[Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V\]$QK^T$得到$N*N$的矩阵,再按行执行$softmax$
最终输出$N \times d_v$大小的矩阵
多头注意力
对于输入的$Q,K,V$
我们对其特征维度按照$h$拆分,这样就变成了$h$组$Q,K,V$
对于每一组进行线性变换后,执行一次Attention
最后,将所有Attention结果concat起来,再进行一次线性变换
公式化表达如下
\[MultiHead(Q,K,V)=Concat(head_1,head_2,\ldots,head_h)W^O \\ head_i=Attention(QW^Q_i,KW^K_i,VW^V_i)\] \[W^Q_i \in \mathbb{R}^{d_{\text{model}} \times d_k}\] \[W^K_i \in \mathbb{R}^{d_{\text{model}} \times d_k}\] \[W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v}\] \[W^O \in \mathbb{R}^{h \cdot d_v \times d_{\text{model}}}\]从$W^O$的维度可以看出,$Concat$是在$head_i$行方向上进行
Attention论文中$h=8$,$d_{model}=512$,$d_v=d_k=\frac{d_{model}}{h}=64$
最终输出大小 $N \times d_{model}$
残差连接与层归一化
公示如下: \(y_{output}=LayerNorm(y_{MultiHead}+x)\)
$y_{MultiHead}$代表多头注意力的输出,$x$代表多头注意力的输入
$LayerNorm$的计算规则如下:
\[LayerNorm(x_i)=\frac{(x_i-\mu)}{\sigma};\mu=\frac{1}{d}\sum_{i}{x_i},\sigma=\sqrt{\frac{1}{d}\sum_{i}{x_i}}\]$x_i$代表一行
最终输出大小 $N \times d_{model}$
以$N=3,d_{model}=512$为例
多头注意力模块的输出大小为$3 \times 512$,输入 $x \in R^{3 \times 512}$,$LayerNorm$输出大小$3 \times 512$
FeedForward&Add&Norm
公式如下: \(y_{output}=LayerNorm(FFN(x)+x)\)
其中FFN公式如下: \(FFN(x)=Activation(xW_0)W_1\)
$w_0 \in R^{512 \times 2048}$,$w_1 \in R^{2048 \times 512}$,Activation如ReLU或GELU
Add&Norm的操作如前所示
最终输出大小$N \times d_{model}$
小结
Encoder层是可以堆叠的,比如选择6层或者12层,每一层的输入输出维度是一样的,最终的输出作为Decoder各层的输入
Decoder
以下模块跟Encoder机制类似,不再赘述
output embedding
positional encoding和encoder
Add&Norm
FFN
掩码多头注意力
与Encoder中的多头注意力机制类似,不同的是这里会使用掩码遮挡未来的输出,不让模型关注
假设此刻Decoder的输入大小为$N_1 \times d_{model}$
输出大小$N_1 \times d_{mdoel}$
交叉注意力
公式表达如下: \(CrossAttention(K,Q,V)=MultiHead(K,Q,V)\)
其中$MultiHead$与Encoder中的表达式一致,不同的是$K$和$V$来自Encoder的输出,两者一致
输出大小$N_1 \times d_{model}$
Linear&softmax
\[y_{output}=Softmax(Linear(x))\]$Linear$负责将$x$中每一个token的特征维度,映射到词汇表大小的维度$d_{voc}$,如下
\[Linear(x)=xW_{voc}\] \[W_{voc} \in R^{d_{model} \times d_{voc}}\]$Softmax$再对每一个toekn的线性映射结果做转换,得到$(0,1)$范围内的概率值
最终输出大小$N_1 \times d_{voc}$
小结
Decoder层可以堆叠,堆叠的层数跟Encoder层可以一致或不一致;对于GPT系列模型,仅需要Decoder层
对于首次token预测,Decoder的输入是起始符
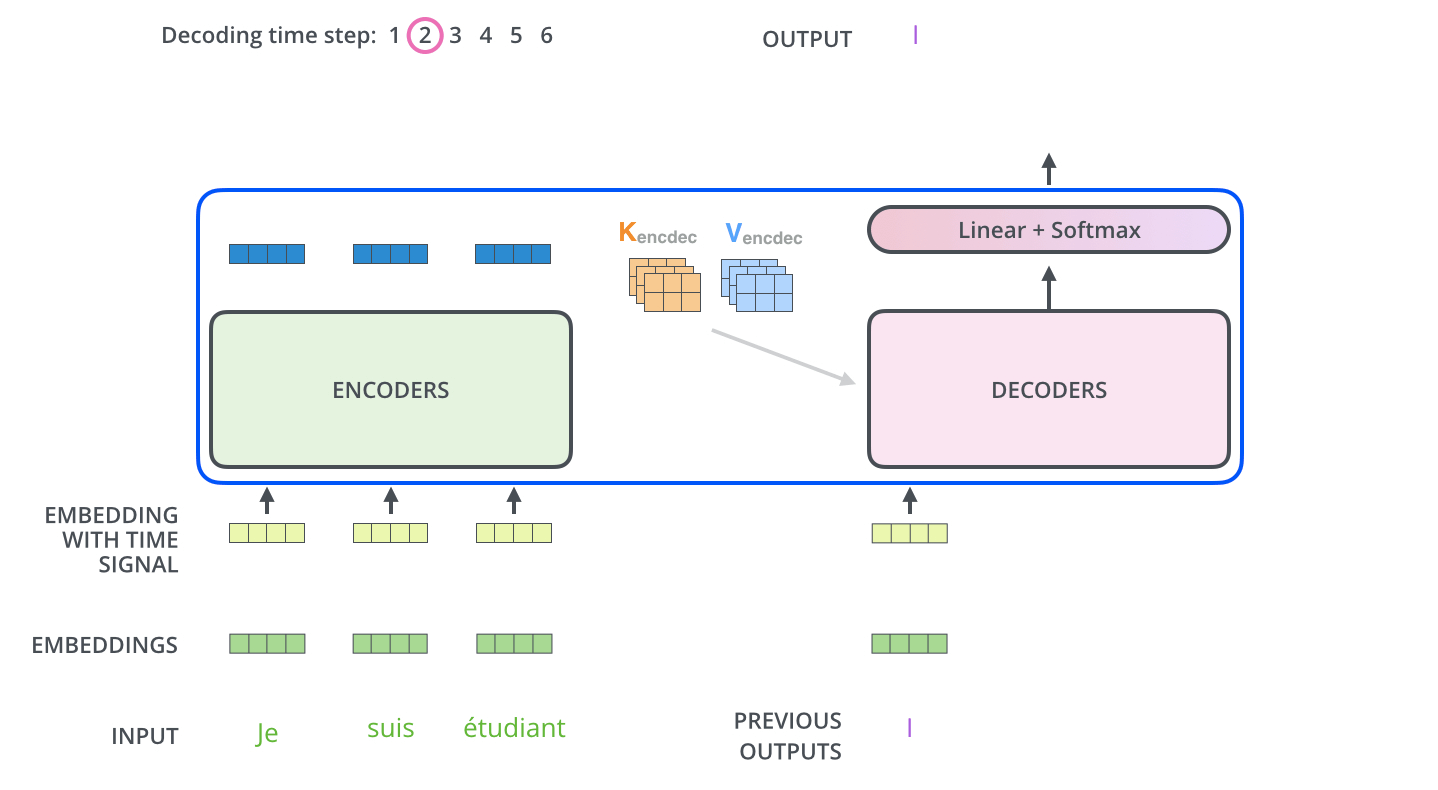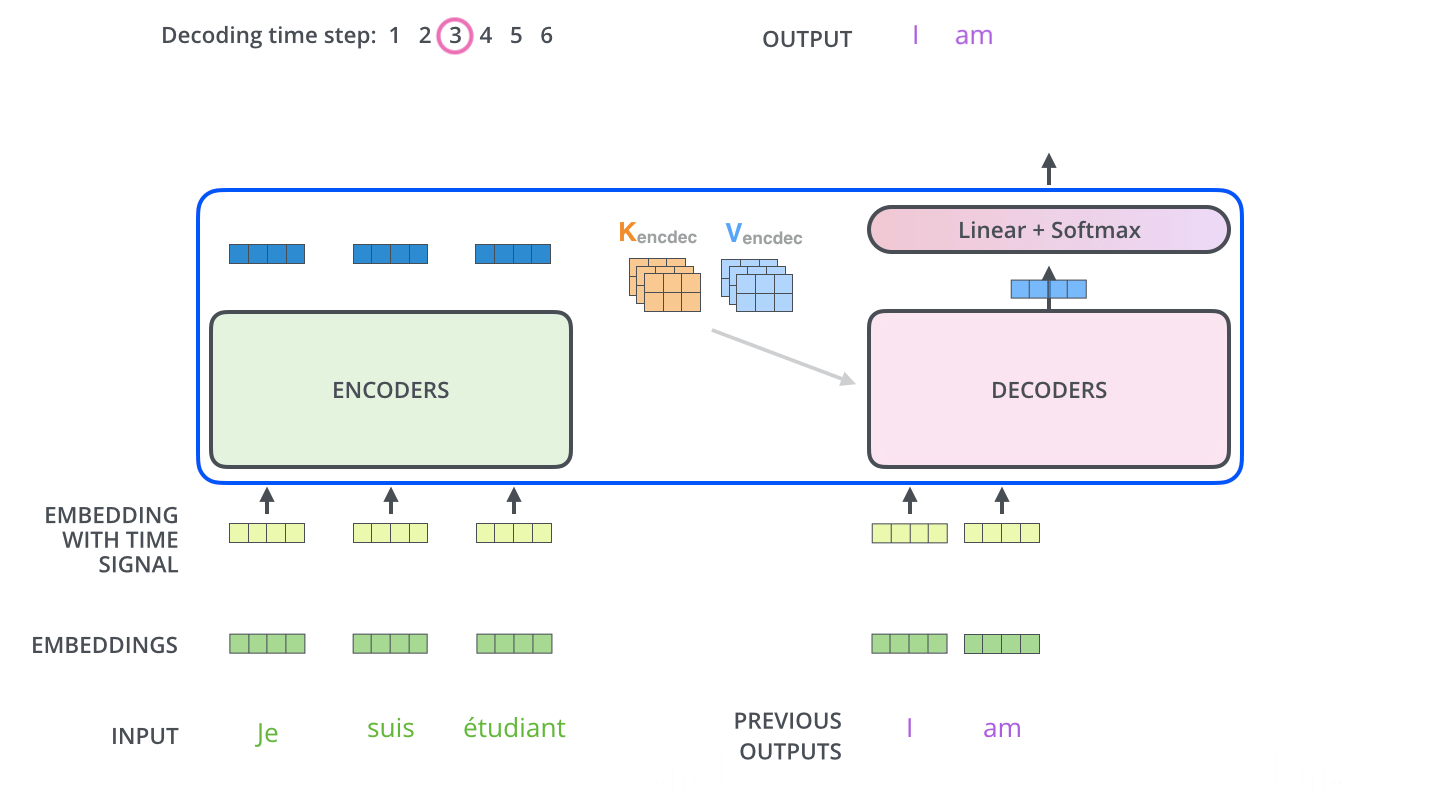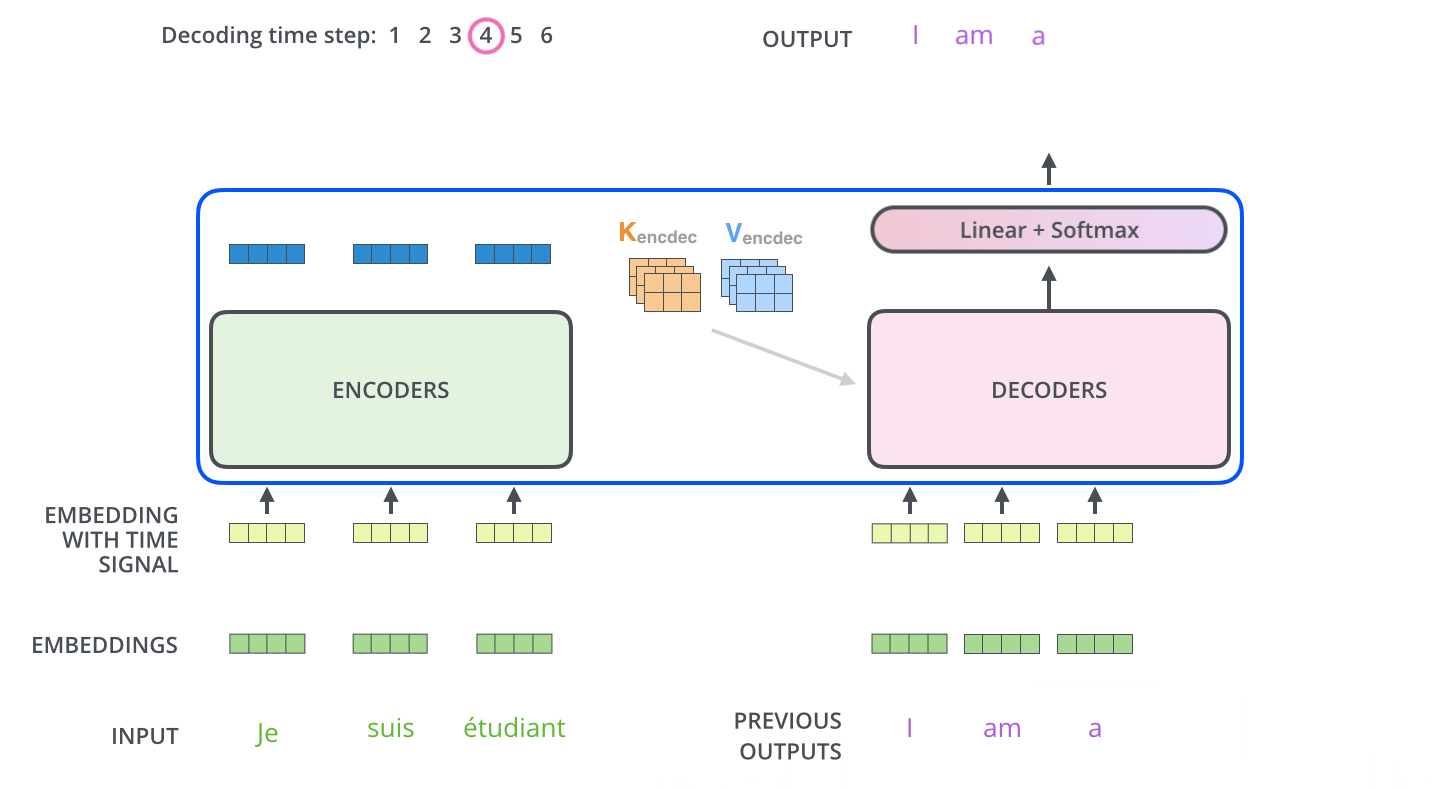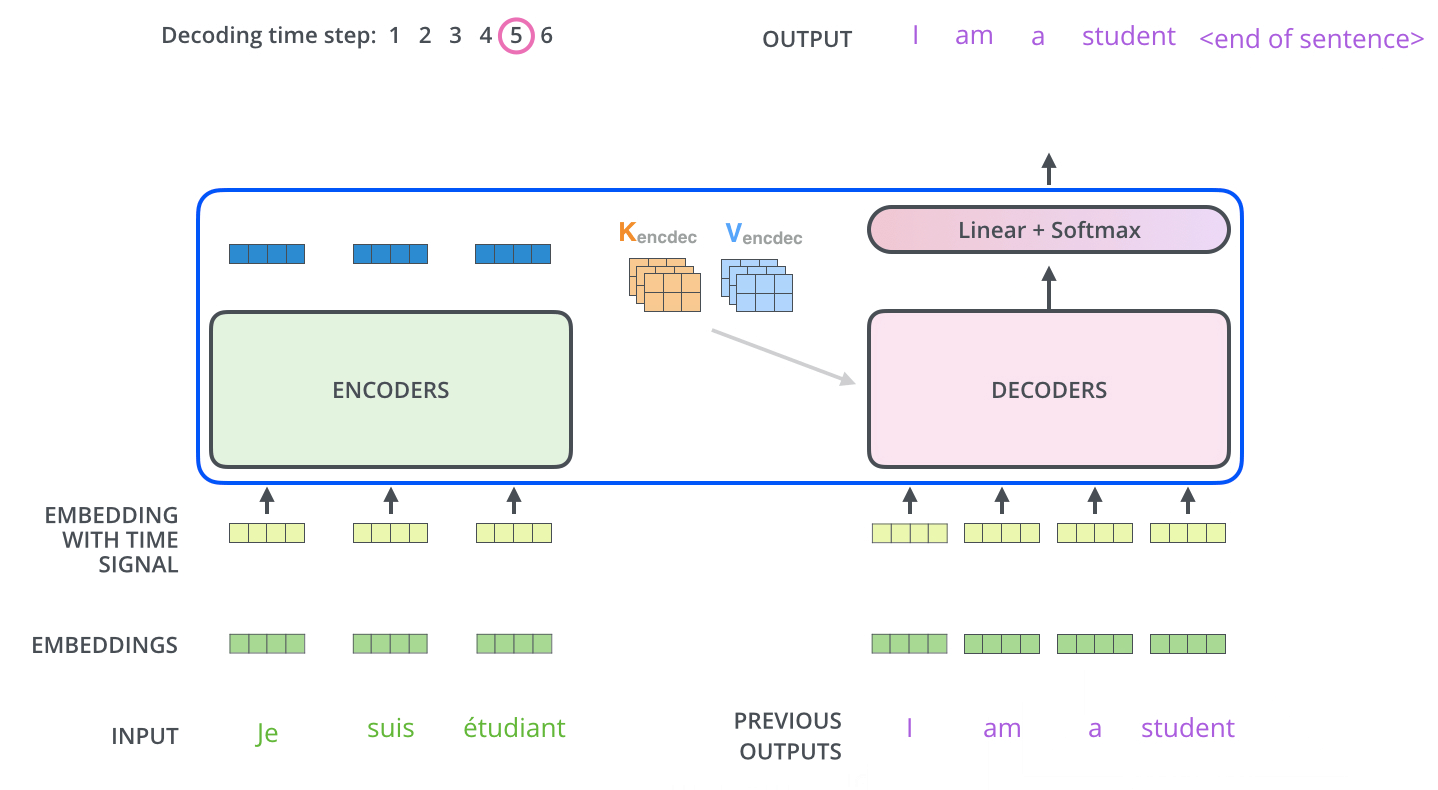
Encoder-Decoder交互动态演示